Понятие о стохастических дифференциальных уравнениях

Стохастическим дифференциальным уравнением (stochastic differential equation) называется уравнение вида (1)

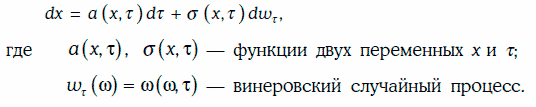
Решением стохастического дифференциального уравнения (1) на промежутке [t, Т] называется случайный процесс х (w, τ), удовлетворяющий следующим условиям:

Любое решение стохастического дифференциального уравнения (1), удовлетворяющее некоторому начальному условию

В частности, геометрическим броуновским движением (geometric Brownian motion) является случайный процесс, удовлетворяющий стохастическому дифференциальному уравнению (2) (3):

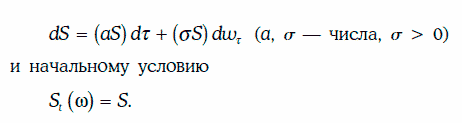
Геометрическое броуновское движение, определяемое условиями (2) и (3), можно найти в явном виде:

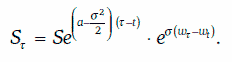
Свойства геометрического броуновского движения

Во многих случаях можно считать, что эволюция цены финансовых активов описывается геометрическим броуновским движением. Такое моделирование оказывается достаточно точным, например, в случае обыкновенных акций.

Пример. Инвестор считает, что цена бездивидендной акции описывается геометрическим броуновским движением с коэффициентом смещения 0,1 и годовой волатильностью 40 %. В данный момент времени цена акции равна 100 долл. Инвестора интересует цена этой акции через месяц.

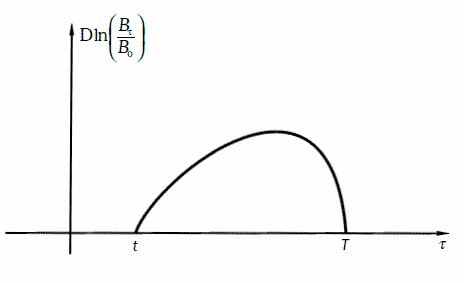
Эволюцию цены Вτ облигации с нулевым купоном можно описывать с помощью геометрического броуновского движения, лишь когда до погашения облигации остается достаточно много времени. Действительно, в момент погашения Т ее цена всегда равна номиналу, т. е. известна достоверно. Это означает, что 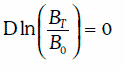 и зависимость  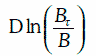от времени должна иметь вид, изображенный на рис. 1.

Таким образом, при моделировании эволюции цены облигации с нулевым купоном необходимо учитывать эффект приближения к номиналу (pull to par), а геометрическое броуновское движение этот эффект не учитывает, так как 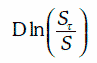 растет во времени линейно.

В общем случае найти решение стохастического дифференциального уравнения (1) в явном виде не удается. Поэтому для моделирования траекторий случайного процесса Ито часто применяется метод Монте-Карло.

Рис. 1.

Чтобы смоделировать траекторию случайного процесса Ито на отрезке [t, Т], этот отрезок разбивается на n равных частей (n должно быть большим), а затем разыгрывается случайная величина м, распределенная нормально с параметрами 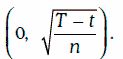 Тогда для последовательности случайных чисел δ1, δ2…., δn будет построена соответствующая последовательность значений  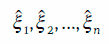случайной величины ξ, а траектория случайного процесса Ито будет определяться точками:

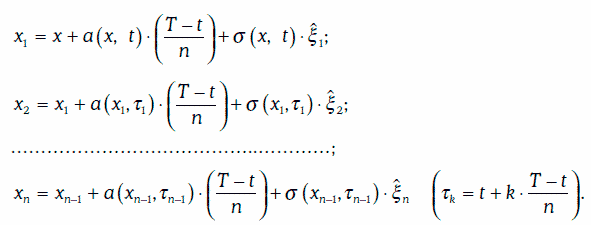
Указанным выше способом можно построить сколь угодно много траекторий случайного процесса Ито.